Hartee-Fock方程式

電子の運動状態と量子化学計算では、電子状態の計算方法としてHartree-Fock法や密度汎関数法があると述べた。本記事ではHartree-Fock法について説明を行う。

Hartree-Fock方程式
1. Hartree-Fock近似
2. 変分原理によるHartree-Fock方程式の導出の流れ
Roothaan方程式
SCF法
まとめ
参考

Hartree-Fock方程式

　下記の記事では、計算を行うとどのようなことが結果が得られるのか述べたが、具体的にどのような計算を行ったかは述べていない。計算方法にはHartree-Fock法や密度汎関数法などがあるのだが、結論から言うと、Hartree-Fock法を量子化学計算ソフトGamessを用いて解いている。Hartree-Fock方程式がどういうものなのか説明して行く。

Hartree-Fock近似

　解きたい方程式はSchrödinger 方程式（(1)式）であるのだが、残念ながら解析的に解くことができるのは水素原子（と水素分子イオン）の場合だけである（※１）。電子が２個以上の場合を考えようとすると多体問題といって数学的に厳密は解を求めることが原理的に不可能だとされている。ヘリウム原子の場合でも電子２個と原子核１個なので３体問題となり近似なしには解けない。そこで独立電子近似（または平均場近似）を導入することで近似解を得ることを考える。独立電子近似は、1つの電子が他の電子が作る平均的な場の中を運動すると考える近似だ。独立電子近似の方法の１つとしてHartree-Fock近似があり、この近似の下では電子の波動関数は(2)式のSlater行列式で表される。Slater行列式は、ハミルトニアン$\hat{H}$が１電子ハミルトニアンの和$\sum_{i=1}^n\hat{H_c}(i)$の形で表せる場合の固有関数となっている。実際の分子では、(3)式のように電子間のクーロン反発の項があるために固有関数ではないが、良い近似になると考えるわけだ。
$$\hat{H}\Psi=E\Psi\tag{1}$$

\begin{eqnarray}
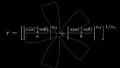
\Psi(\tau_1, \tau_2, \cdots, \tau_2)=\frac{1}{\sqrt{n!}}
\begin{vmatrix}
\psi_1(\tau_1) & \psi_2(\tau_1) & \cdots & \psi_n(\tau_1) \\
\psi_1(\tau_2) & \psi_2(\tau_2) & \cdots & \psi_n(\tau_2) \\
\ & \cdots & \cdots & \\
\psi_1(\tau_n) & \psi_2(\tau_n) & \cdots & \psi_n(\tau_n) \tag{2}
\end{vmatrix}
\end{eqnarray}

$$\hat{H}=\displaystyle \sum_{i=1}^n\hat{H_c}(i)+\sum_{i>j}^n \frac{1}{r_{ij}}\\
=(一電子ハミルトニアンの和)+(電子間クーロン反発) \tag{3}$$

※１：この時点でBorn–Oppenheimer近似成り立つ仮定の下議論している。基底状態の分子を考える場合においてはこの近似は常に成り立つと考えてよい。化学反応など原子核の位置がダイナミックに変化する現象を考える際はBorn–Oppenheimer近似が成り立たなくなる場合がある。　

変分原理によるHartree-Fock方程式の導出の流れ

　基底状態をよく表す最良のSlater行列式は最低エネルギーを与えるはずだから、エネルギーについて変分法を用いると、基底状態を表すSlater行列式の満たす方程式が得られる。エネルギーは(1)式の左から波動関数の複素共役を掛けて積分すると次式となる。
$$E=\frac{\int\Psi^{*}\hat{H}\Psi d\tau}{\int\Psi^{*}\Psi d\tau} \tag{4}$$
さらに$\psi_1,\psi_2,\cdots,\psi_n$が正規直交性を持つと仮定すると
$$E=\int\Psi^{*}\hat{H}\Psi d\tau\tag{4′}$$
となる。これの最小値を変分法で求めると(5)式にHartree-Fock方程式が得られる。
$$\hat{F}\psi_{i}=\displaystyle \sum_{j=1}^n\varepsilon_{ij}\psi_{j}\tag{5}$$
$\hat{F}$はFock演算子で
$$\hat{F}\equiv\hat{H}_c+\displaystyle \sum_{j=1}^n(\hat{J}_j-\hat{K}_j)\tag{6}$$
で定義され、$\hat{J}_j,\hat{K}_j$は、

$$\hat{J}_j(\tau_1)\psi(\tau_1)\equiv\int\frac{\psi_{j}^{*}(\tau_2)\psi_{j}(\tau_2)}{r_{12}}d\tau_2\cdot\psi(\tau_1)\tag{7}$$

$$\hat{K}_j(\tau_1)\psi(\tau_1)\equiv\int\frac{\psi_{j}^{*}(\tau_2)\psi(\tau_2)}{r_{12}}d\tau_2\cdot\psi_{j}(\tau_1)\tag{8}$$

で定義される。(6)式は適当なユニタリ変換によって次の正準型に変換される。
$$\hat{F}\psi_{i}=\varepsilon_{i}\psi_{i} \qquad i=1,2,\cdots,n \tag{9}$$
　(9)式をを解くことで独立電子近似のもとで最良の結果が得られる。

Roothaan方程式

　(9)式は連立微分方程式であるため、計算機でそのまま計算するには向かない。計算機で計算するに適した形の方程式にすることを考える。まず、簡単のために閉殻の場合だけを扱うことにする。閉殻というのはエネルギーの低い方から同じ空間軌道関数をαスピンとβスピンの電子が対を作って占有することだから、1電子波動関数$\psi_{i}$を空間軌道関数とスピン軌道関数の積で$\phi_{i}\alpha$または$\phi_{i}\beta$で表現したとき、(9)式の空間軌道関数による表現は

$$\hat{F}\phi_{i}=\varepsilon_{i}\phi_{i} \qquad i=1,2,\cdots,n/2 \tag{10}$$

となる。ここで空間軌道関数$\phi_{i}$を基底関数系$\chi_{\mu} \ (\mu=1,2,\cdots,m)$で展開して

$$\phi_{i}=\displaystyle \sum_{\mu=1}^mc_{\mu i}\chi_{\mu}\tag{11}$$

と表現することで、連立微分方程式を解いて$\phi_{i}$を求める問題から、連立方程式を解いて展開係数$c_{\mu i}$問題を求める問題へと変換することができる。解くべき式は

$$\displaystyle \sum_{\nu=1}^m(F_{\mu\nu}-\varepsilon_{i}S_{\mu\nu})c_{\nu i}=0\qquad \mu,i=1,2,\cdots,m\tag{12}$$

$$F_{\mu\nu}\equiv H_{\mu\nu}^c+\displaystyle \sum_{\lambda, \sigma=1}^mP_{\lambda \sigma}\left[(\mu\nu|\lambda \sigma)-\frac{1}{2}(\mu\sigma|\lambda \nu)\right]\tag{13}$$

$$H_{\mu\nu}^c\equiv \int \chi_{\mu}^{*}(1) \hat{H_{c}}(1) \chi_{\nu}(1)dv_1 \tag{14}$$

$$P_{\lambda \sigma}\equiv 2 \displaystyle \sum_{j=1}^{n/2} c_{\lambda j}^{*} c_{\sigma j}\tag{15}$$

$$(\mu\nu|\lambda \sigma) \equiv \int \frac{\chi_{\mu}^{*}(1) \chi_{\nu}(1) \chi_{\lambda}^{*}(2) \chi_{\sigma}(2)}{r_{12}} dv_1 dv_2 \tag{16}$$

$$S_{\mu\nu} \equiv \int \chi_{\mu}^{*}(1) \chi_{\nu}(1)dv_1 \tag{17}$$

となり、(12)式をRoothaan方程式という。

SCF法

　(12)式を計算機を使って解くにあたって、もう一度式の形をよく見てほしい。いま求めたいのは基底関数系での展開係数$c_{\nu i}$だ。しかし、よく見ると(13)式で定義されるFock行列の中に$c_{\nu i}$が含まれているのである。求める答えが得られないと解くべき方程式が定まらないというジレンマにあることがわかる。言ってみればこの方程式はそもそも厳密な解を得ることができないので、どうにか近似解を得ようというのが自己無撞着場 (SCF; Self-Consistent Field)の方法である。SCF法では、まず初期軌道関数を仮定してやることで解を得て、その解を再び方程式に代入して解くという過程を繰り返し行うことで徐々に真の解に近づいて行く。初期軌道関数は、経験的分子軌道法という繰り返し解法によらない方法で生成するのが普通である。最後にある軌道係数に収束すれば、それを求める解として一件落着となる。

まとめ

　Hartree-Fock方程式がどういったもので、計算機の中でどのようなことが行われているか何となくわかって頂けただろうか。実際このようなことを知らなくてもソフトウェアに条件を入力してしまえば何らかの答えは得ることができるのだが、やはりこのようなバックグラウンドを知っていないと出力されたファイルの中身を見て妥当な答えが得られたのか判断することができないと思う。もっと実践的な内容は別な記事にしようと思う。

参考

原田義也. 量子化学. 下巻. 第１版, 裳華房, 2007, 131-167.