アルカンの異性体の数え上げをPythonでやってみる

isomer_enumeration グラフ理論


　有機化学を学ぶと最初に出会う化合物の族がアルカン\( \rm C_{n}H_{2n+2}\)だと思う。そして、よく高校の教科書や資料集にアルカンの異性体の数が載っていることがある。私も高校生の時に資料集にアルカンの異性体の数が載っていて、どうやって計算したんだろうと思った記憶がある。何らかの漸化式を立てて、一般項をもとめることはできるのだろうか？などと思ったものだ。結論から言おう、異性体の数を表すための簡単な公式は存在しない。だからと言って数えることができないわけではない。ここではPólyaという数学者の理論をPythonコード化して異性体の数の数え上げをやってみる。

アルカンとは

　化学系の方だけではないと思うので簡単に説明しておくと、アルカンとは\( \rm C_{n}H_{2n+2}\)の一般式で表される炭化水素で、炭素数n=1からメタン、エタン、プロパン、ブタン、…という名称の化合物の族だ。ここでいうアルカンには環状のもの（シクロアルカン\( \rm C_{n}H_{2n}\)）は含まない。

異性体とは

　異性体についても簡単に述べておく。例えば、炭素数4のブタンには直鎖構造のn-ブタン（ノルマルブタン）と枝分かれした構造のi-ブタン（イソブタン）の2種類の異性体が存在する。ブタンの場合は２種類だけだが、異性体の数は炭素数が増加するにつれて指数関数的に増大する。そのため、炭素数が少ないうちは異性体の数え上げは手計算でも可能だが、炭素数が増えるにつれ困難になる。（炭素数11の時点で異性体の数は100を超える）

n-butane
図１(a) n-ブタン

i-butane
図1(b) i-ブタン

化学とグラフ理論

歴史

　化学とグラフ理論の関わりの歴史についても触れておきたい。結論だけ知りたい人は読み飛ばして頂いて構わない。
　19世紀終わりに、化合物を数学的なグラフとして解釈して異性体の数え上げができることに最初に気が付いたのはイギリス人の数学者Cayleyだった。その後1930年代に、アメリカ人科学者のHanzeとBlairによってCayleyのアイデアは精緻化され、アルカンの異性体の数を正しく与えることに成功した。
　その後、1935年にハンガリーの数学者Pólya（ポリア）が巡回指数（cycle index）や数え上げ多項式（counting polynomial）といった群論及びグラフ理論の概念を用い、アルカンやその他化合物の数え上げを行うための体系化された手法を発表した。

用語の整理

　本題に入る前に用語の整理をしておく。ここで全てを説明することはできないが基本的な用語については化学とグラフ理論の間で表１の対応がある。

表１　用語の対応
化学 グラフ理論
原子 点
化学結合 線
分子 グラフ
非環状分子 木

　また、ここで詳しい説明はできないが、対称群\(S_{2},S_{3},S_{4}\)の巡回指数\(Z\)の具体的な形を記しておく。後述の計算で、順序付けられていないN個の組を選ぶときは\(S_{N}\)を群として選択することになる。

\begin{align}
&Z(S_{2})=&(y_{1}^2+y_{2})/2 \\
&Z(S_{3})=&(y_{1}^3+3y_{1}y_{2}+2y_{3})/6 \\
&Z(S_{4})=&(y_{1}^4+6y_{1}^2y_{2}+8y_{1}y_{3}+3y_{2}^2+6y_{4})/24
\end{align}

例えば、多項式\(P(x)\)を\(Z(S_{2})\)に代入するときは、
\begin{align}
Z (S_{2};P(x)) \ =\frac {\{P(x)\} ^{2}+P( x^{2}) }{2}\\
\end{align}

を計算すれば良い。

Pólyaの理論

アルコールの数え上げ多項式

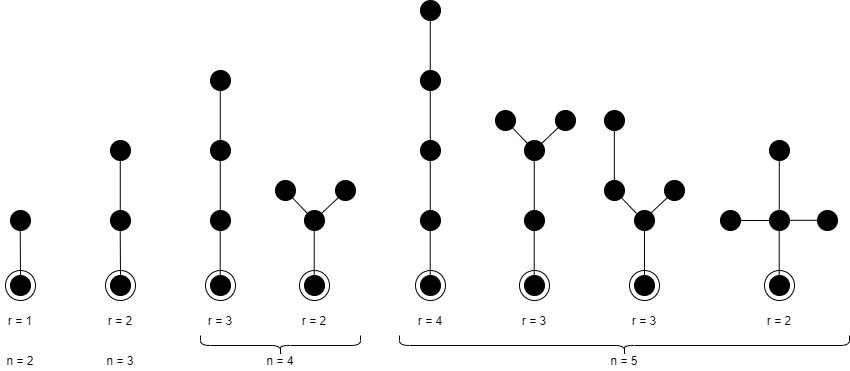
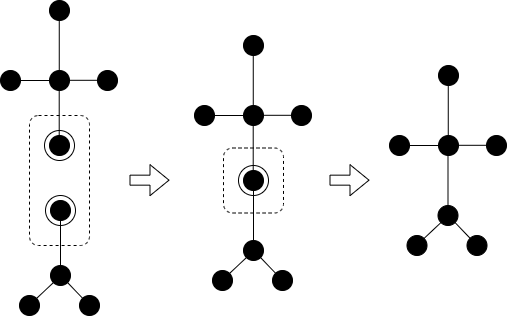
　アルカンの数え上げを行うのに何故アルコールの話をするのかと思われると思うが、それが関係あるのだ。異性体の数え上げの基本的なアイデアとしてplanted treeというものの数え上げを行い、これの組み合わせを考えるという方法を取る。planted treeというのは次数1（※）の特別な1点を持つ木のことで、アルカンを木と考えた時、対応するplanted treeはOH基が特別な点と見なすことで1価のアルコールと考えることができる（図2）。planted treeの直径rは、主鎖の単結合の数のことである。
※：ある点から出る線の数を次数という。

rooted_graph
図２　n=1～4の1価アルコールを表すplated tree（○が付いた点がOH基）

　アルコールの数え上げ多項式は次式の形をしている。

\begin{align}
P_{r}=\sum_{n\geq 0}p_{n,r}x^{n}
\end{align}

係数\(p_{n,r}\)は炭素数n、直径rの異性体の数を表している。例えば、図２から
\begin{align}
P_{2}=x^3 + x^4 + x^5
\end{align}

となる。
この数え上げ多項式は次式から再帰的に得ることができる。この式はこういうものだと認めた上で話を進める。（私が説明できないので）
\begin{align}
P_{r}=xP_{r-1}+Z (S_{2};P_{r-1}(x)) + P_{r-1} (x)W_{r-2}(x) \\
+x^{-1}Z(S_{3};P_{r-1}(x))+Z(S_{2};P_{r-1}(x))W_{r-2}(x) \tag{1}\\
+P_{r-1}(x) Z( S_{2};W_{r-2}(x))
\end{align}

ここで、
\begin{align}
W_{r-1}=\sum_{i=1}^{r-1}P_{i}(x)\tag{2}
\end{align}

アルケンの数え上げ多項式

　さて、\(P_{r}\)が得られたので次はいよいよアルケンの数え上げ多項式

\begin{align}
A_{d}=\sum_{n\geq 0}a_{n,d}x^{n}
\end{align}

を計算する段階となる。係数\(a_{n,d}\)は炭素数n、直径（主鎖の単結合の数）dの異性体の数を表している。\(A_{d}\)は、直径dが奇数2r-1の場合と偶数2rの場合に分けて考える必要がある。

d=2r-1の場合

　いきなり一般の場合を考えるのではなくd=3を構成することを考えてみよう。d=3のアルカンを構成するには２つのr=2のアルコールより図３の手順で行う。
①2つのr=2のアルコールを用意する。
②アルコールのOH基同士を重ねて1つの点と見なす。
③OH基を除去して炭素原子同士を線で結ぶ。
これによりd=2r-1=3のアルカンを構成できる。

図３　d=3のアルカンの構成方法の一例

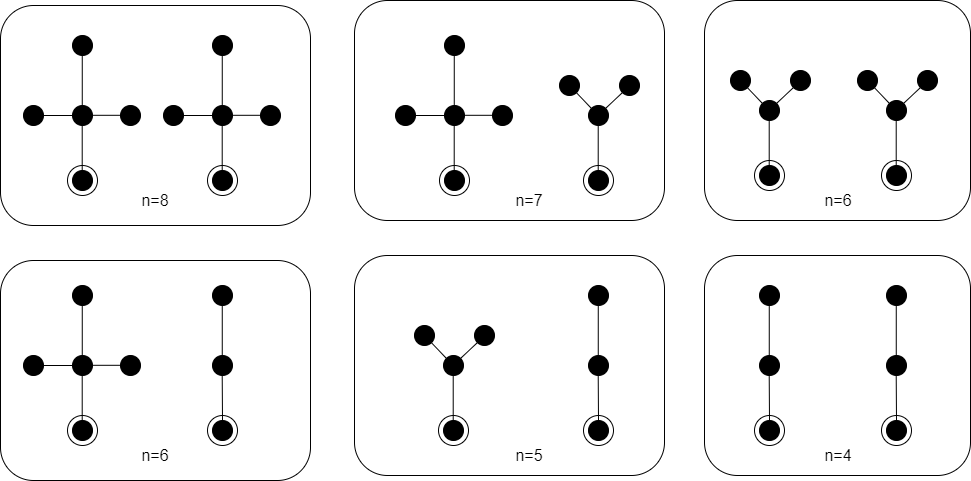
　d=3のアルカンを構成するアルコールの組み合わせは図４の6種類があるので、

\begin{align}
A_{3}=x^4 + x^5 + 2x^6 + x^7 + x^8
\end{align}

と結論できる。

図4　d=3のアルカンの構成の組み合わせ

上記①～③の手順は、数え上げ多項式で表現することができて、以下のようになる。
①巡回指数\(Z (S_{2})\)への数え上げ多項式\(P_{2}\)を代入する。

\begin{align}
Z (S_{2};P_{2}) \ =\frac {\{P_{2}(x)\} ^{2}+P_{2}( x^{2}) }{2}\\
\qquad =x^6 + x^7 + 2x^8 + x^9 + x^{10}
\end{align}

②③\(x^2\)で割る。これは点が２つ減ることに対応している。
\begin{align}
A_{3}=x^{-2}Z (S_{2};P_{2})=x^4 + x^5 + 2x^6 + x^7 + x^8
\end{align}

以上の議論は一般のdについても拡張出来て
\begin{align}
A_{2r-1}=x^{-2}Z (S_{2};P_{r})\tag{3}
\end{align}

となる。

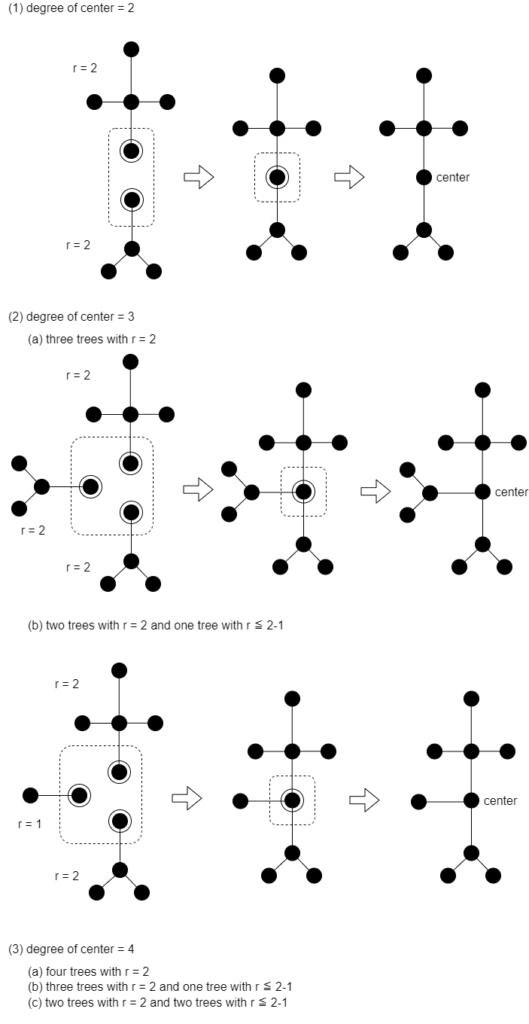
d=2rの場合

　dが偶数の場合は図5（d=4の例）のようにアルコールからアルカンを組み立てる。中心（center）の次数が2, 3, 4の場合があるので(1)～(3)の場合分けが必要になる。さらに(2)は(a),(b)の場合に分かれ、(3)は(a),(b),(c)の場合に分かれる。それぞれの場合を組み合わせ多項式で表現すると、

\begin{align}
&(1)& \qquad x^{-1}Z (S_{2};P_{r}) \\
&(2)(a)& \qquad x^{-2}Z (S_{3};P_{r}) \\
&(2)(b)& \qquad x^{-2}Z (S_{2};P_{r})W_{r-1} \\
&(3)(a)& \qquad x^{-3}Z (S_{4};P_{r}) \\
&(3)(b)& \qquad x^{-3}Z (S_{3};P_{r})W_{r-1} \\
&(3)(c)& \qquad x^{-3}Z (S_{2};P_{r})Z (S_{2};W_{r-1}) \\
\end{align}

したがって、\(A_{2r}\)はこれらの和で
\begin{align}
A_{2r}=x^{-1}Z (S_{2};P_{r}) + x^{-2} \{ Z (S_{3};P_{r})+Z (S_{2};P_{r})W_{r-1} \} \qquad \qquad\tag{4}\\
+x^{-3} \{ Z (S_{4};P_{r}) + Z (S_{3};P_{r})W_{r-1} +Z (S_{2};P_{r})Z (S_{2};W_{r-1}) \}
\end{align}

図5　d=4のアルカンの構成の組み合わせ

数え上げの実行

やること

　説明が長くなったが、やることとしては(1),(2)式で\(P_{r}\)を計算し、(3),(4)式で\(A_{d}\)を計算するというだけだ。式がちょっと複雑な形をしているだけで、やっていることは多項式の代入と展開を繰り返しているというシンプルなものだ。

コード

from sympy import Symbol, expand
import pandas as pd

x = Symbol('x')
P1 = Symbol('P1')
P_old = Symbol('P_old')
P_new = Symbol('P_new')
W_old = Symbol('W_old')
W = Symbol('W')
A_odd = Symbol('A_odd')
A_even = Symbol('A_even')

#係数を格納するリスト
coeff = [[0 for i in range(21)] for  j in range(20)]
for k in range(1, 21):
    if k == 1 :
        coeff[k-1][0] = 1
    else:
        coeff[k-1][0] = 0

################
# A1, A2の計算  #
################
P1 = x**2
W = 0

A_odd = (P1**2 + P1.subs([(x, x**2)]))/(2*x**2)
A_even = (P1**2 + P1.subs([(x, x**2)]))/(2*x) +\
(1/(6*x**2)) * (P1**3 + 3*P1*P1.subs([(x, x**2)]) + 2*P1.subs([(x, x**3)])) +\
(1/(2*x**2)) * (P1**2 + P1.subs([(x, x**2)]))*W +\
(1/(24*x**3)) * (P1**4 + 6*(P1**2)*P1.subs([(x, x**2)]) + 8*P1*P1.subs([(x, x**3)]) + 3*P1.subs([(x, x**2)])**2 + 6*P1.subs([(x, x**4)])) +\
(1/(6*x**3)) * (P1**3 + 3*P1*P1.subs([(x, x**2)]) + 2*P1.subs([(x, x**3)])) * W +\
(1/(4*x**3)) * (P1**2 + P1.subs([(x, x**2)]))*(W**2)

for k in range(1, 21):
    coeff[k-1][1] = expand(A_odd).coeff(x, k)
    coeff[k-1][2] = expand(A_even).coeff(x, k)

################
# A3, A4の計算  #
################

#１：値をセット
W_old = 0
W = W_old + P1
P_old = P1

#２：新しいPを計算
P_new = \
x*P_old + \
(P_old**2 + P_old.subs([(x, x**2)]))/2 + \
P_old*W_old + \
(1/(6*x)) * (P_old**3 + 3*P_old*P_old.subs([(x, x**2)]) + 2*P_old.subs([(x, x**3)])) +\
(1/(2*x)) * (P_old**2 + P_old.subs([(x, x**2)]))*W_old +\
P_old * (1/(2*x)) * (W_old**2)

#３：新しいAを計算
P= 0
for i in range(0, 21):
    P += expand(P_new).coeff(x, i) * x**i 
    
A_odd = (P_new**2 + P_new.subs([(x, x**2)]))/(2*x**2)
A_even= (P**2 + P.subs([(x, x**2)]))/(2*x) +\
(1/(6*x**2)) * (P**3 + 3*P*P.subs([(x, x**2)]) + 2*P.subs([(x, x**3)])) +\
(1/(2*x**2)) * (P**2 + P.subs([(x, x**2)]))*W +\
(1/(24*x**3)) * (P**4 + 6*(P**2)*P.subs([(x, x**2)]) + 8*P*P.subs([(x, x**3)]) + 3*P.subs([(x, x**2)])**2 + 6*P.subs([(x, x**4)])) +\
(1/(6*x**3)) * (P**3 + 3*P*P.subs([(x, x**2)]) + 2*P.subs([(x, x**3)])) * W +\
(1/(4*x**3)) * (P**2 + P.subs([(x, x**2)]))*(W**2 + W.subs([(x, x**2)]))


#４：係数を保存
for k in range(1, 21):
    coeff[k-1][3] = expand(A_odd).coeff(x, k)
    coeff[k-1][4] = expand(A_even).coeff(x, k)

################
# A5以降の計算  #
################


for j in range(1,9):
    #１：値をセット
    W_old = W_old + P_old #P_1+...+P_r-2
    W = W_old + P_new #P_1+...+P_r-1
    P_old = 0
    for i in range(0, 21):
        P_old += expand(P_new).coeff(x, i) * x**i 

    #２：新しいPを計算
    P_new = \
    x*P_old + \
    (P_old**2 + P_old.subs([(x, x**2)]))/2 + \
    P_old*W_old + \
    (1/(6*x)) * (P_old**3 + 3*P_old*P_old.subs([(x, x**2)]) + 2*P_old.subs([(x, x**3)])) +\
    (1/(2*x)) * (P_old**2 + P_old.subs([(x, x**2)]))*W_old +\
    P_old * (1/(2*x)) * (W_old**2 + W_old.subs([(x, x**2)]))

    #３：新しいAを計算
    P= 0
    for i in range(1, 21):
        P += expand(P_new).coeff(x, i) * x**i 

    A_odd = (P**2 + P.subs([(x, x**2)]))/(2*x**2)
    A_even= (P**2 + P.subs([(x, x**2)]))/(2*x) +\
    (1/(6*x**2)) * (P**3 + 3*P*P.subs([(x, x**2)]) + 2*P.subs([(x, x**3)])) +\
    (1/(2*x**2)) * (P**2 + P.subs([(x, x**2)]))*W +\
    (1/(24*x**3)) * (P**4 + 6*(P**2)*P.subs([(x, x**2)]) + 8*P*P.subs([(x, x**3)]) + 3*P.subs([(x, x**2)])**2 + 6*P.subs([(x, x**4)])) +\
    (1/(6*x**3)) * (P**3 + 3*P*P.subs([(x, x**2)]) + 2*P.subs([(x, x**3)])) * W +\
    (1/(4*x**3)) * (P**2 + P.subs([(x, x**2)]))*(W**2 + W.subs([(x, x**2)]))

    #４：係数を保存
    for k in range(1, 21):
        coeff[k-1][2*(j+2)-1] = expand(A_odd).coeff(x, k)
        coeff[k-1][2*(j+2)] = expand(A_even).coeff(x, k)

#各炭素数における合計を計算
for j in range(0,20):
    for k in range(0, 20):
        coeff[j][20] += coeff[j][k]
index = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
columns = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,'Total']
df = pd.DataFrame(data=coeff, index=index, columns=columns)  
df.to_html('isomer_enumeration.html')
print(df)

結果

　n行d列が\(a_{n,d}\)に対応している。Totalの列のn行目が炭素数nの異性体の数に対応している。参考文献3に記載の値と一致していることが確認出来た。

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Total
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
3 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
4 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2
5 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
6 0 0 0 2 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5
7 0 0 0 1 5 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 9
8 0 0 0 1 6 7 3 1 0 0 0 0 0 0 0 0 0 0 0 0 18
9 0 0 0 0 8 12 11 3 1 0 0 0 0 0 0 0 0 0 0 0 35
10 0 0 0 0 7 23 26 14 4 1 0 0 0 0 0 0 0 0 0 0 75
11 0 0 0 0 7 30 59 39 19 4 1 0 0 0 0 0 0 0 0 0 159
12 0 0 0 0 5 42 109 108 62 23 5 1 0 0 0 0 0 0 0 0 355
13 0 0 0 0 5 47 196 244 191 84 29 5 1 0 0 0 0 0 0 0 802
14 0 0 0 0 3 55 313 532 503 293 118 34 6 1 0 0 0 0 0 0 1858
15 0 0 0 0 2 53 485 1047 1252 867 442 151 41 6 1 0 0 0 0 0 4347
16 0 0 0 0 1 53 700 1986 2880 2426 1439 621 198 47 7 1 0 0 0 0 10359
17 0 0 0 0 1 45 982 3533 6337 6259 4375 2193 862 244 55 7 1 0 0 0 24894
18 0 0 0 0 0 40 1306 6086 13262 15451 12364 7224 3267 1146 306 62 8 1 0 0 60523
19 0 0 0 0 0 29 1703 10021 26835 36304 33312 22039 11452 4633 1509 367 71 8 1 0 148284
20 0 0 0 0 0 23 2129 16047 52411 82471 85754 64000 37271 17284 6464 1930 446 79 9 1 366319

まとめ

　数え上げ多項式を使うと漏れなくダブりなく異性体の数を数え上げられることがわかる。機械的に多項式を展開するだけで数え上げができるというのは驚くべきことではないだろうか。数え上げの数学は化学科では教わることは現状まずないのだが、もっと化学者に広まっていくべき内容だと思う。

参考

  1. 細谷治夫. はじめての構造化学. 第１版, オーム社, 2013.
  2. BLAIR, Charles M.; HENZE, Henry R. The number of stereoisomeric and non-stereoisomeric paraffin hydrocarbons. Journal of the American Chemical Society, 1932, 54.4: 1538-1545.
  3. BALABAN, Alexandru T.; KENNEDY, John W.; QUINTAS, Louis. The number of alkanes having N carbons and a longest chain of length D: an application of a theorem of Polya. Journal of Chemical Education, 1988, 65.4: 304.
タイトルとURLをコピーしました